جلسهی چهارم: فواصل کاسته، افزوده، ترکیبی- مطبوع و نامطبوع
در این جلسه، نکات بیشتری درمورد فواصل گفته شدهاست و فاکتورهای مهم دیگری را، جدا از مطبوع یا نامطبوع بودن فواصل، خواهید آموخت.
در جلسهی سوم تئوری موسیقی، درمورد عدد فاصله و فواصل موجود در گامهای ماژور و مینور طبیعی (با شروع از نت تونیک) صحبت کردیم.
در گام «دو ماژور» و «دو مینور طبیعی» (که با نتهای سیاه نشان داده شدهاند)، فواصل زیر را داریم:

شایان ذکر است که فواصل کوچک (مینور)، نیمپرده کوچکتر از فواصل بزرگ (ماژور)، با همان شمارهی فاصله، هستند.
تا اینجای کار اطلاعات گستردهای را در زمینهی فواصل موسیقیایی آموختهایم، اما فواصلی که در خارج از گام ماژور یا مینور طبیعی وجود دارند چه میشوند؟ فواصل «دو» تا «فا دیز» یا «دو» تا «سل بمل» که نه در گام «دو ماژور» و نه در گام «دو مینور» وجود دارند، چگونه نامگذاری میشوند؟
فواصلی که در گام ماژور یا مینور پدیدار میشوند اما هنوز شیوهی محاسبهی آنها را نیاموختهایم چطور؟ مانند فاصلهی چهارمی که در تصویر زیر، در گام «دو ماژور» وجود دارد:

با توجه به روشی که در جلسهی گذشته آموختیم، که نت بم را بهعنوان نت تونیک بدلی بهحساب میآوردیم و فاصله را باتوجه به آن محاسبه می کردیم (مشاهدهی روش)، در اینجا؛ نت «فا» را بهعنوان نت تونیک درنظر میگیریم. این فاصله میتوانست یک فاصلهی «چهارم درست» باشد. اما از آنجاییکه نت «سی» بکار است و «سی بمل» نیست، پس در گام «فا ماژور» وجود ندارد و فاصلهی چهارم درست نیست.
با توجه به اینکه فاصلهی بین «فا» تا «سی»، نیمپرده بزرگتر از فاصلهی چهارم درست است، به آن «فاصلهی چهارم افزوده» گفته میشود.
هر فاصلهی درست که نیمپرده افزایش یابد، به فاصلهی افزوده (Augmented) تبدیل میشود.
فاصلهی «دو» تا «فا دیز» که در جلسهی گذشته به آن اشاره کردیم نیز یک فاصلهی چهارم افزوده است. از آنجاییکه این فاصله از سه پرده تشکیل شدهاست، به آن فاصلهی تریتون (Tritone – سه پردهای) نیز گفته میشود.
فاصلهی چهارم افزوده (Augmented 4th/ Tritone)، کاراکتری نامطبوع و ناپایدار دارد. در قرونوسطی، از فاصلهی چهارم افزوده استفاده نمیکردند، چراکه اعتقاد داشتند این فاصله نماد شیطان در موسیقی است. (Diabolus in musica)
بیایید ایندفعه، همین فاصله را در حالت عکس بررسی کنیم: (نت «فا» را زیرتر از نت «سی» اجرا کنیم)

اگر نت «سی» را بهعنوان تونیک درنظر بگیریم، فاصلهی نت «سی» تا «فا دیز»، «فاصلهی پنجم درست» خواهدبود.
و از آنجاییکه فاصلهی نت «سی» تا «فا بکار»، نیمپرده از «فاصلهی پنجم درست» کوچکتر است، به آن «فاصلهی پنجم کاسته» (Diminished) گفته میشود.
در مثال زیر سه مدل فاصلهی اکتاو (هشتم) را میبینیم:
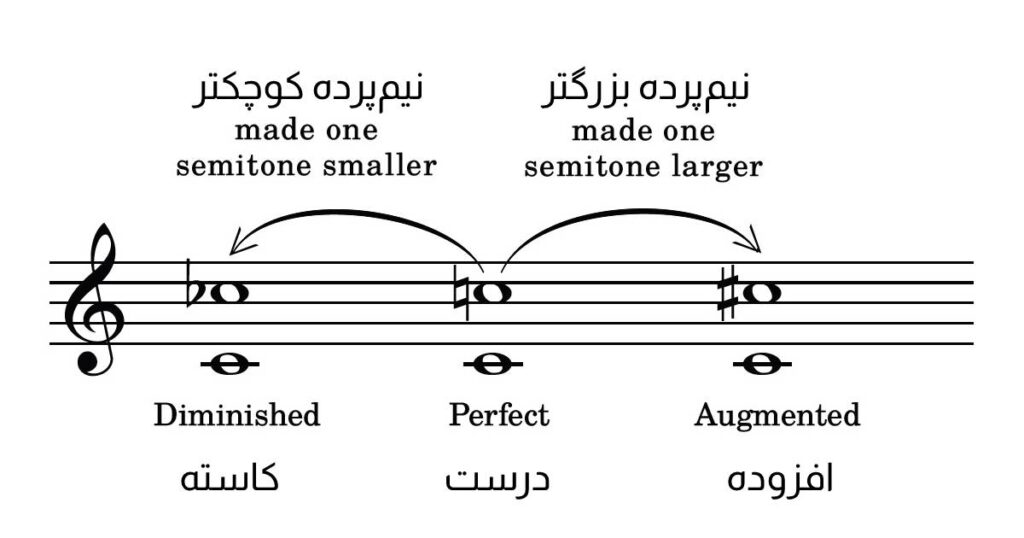
این قانون فواصل کاسته و افزوده، برای فواصل کوچک (Minor) و بزرگ (Major) نیز صدق میکند.
به مثالهای دوم (b) و سوم (c) در تصویر زیر، که «فاصلهی دوم کوچک» و «فاصلهی دوم بزرگ» را نشان میدهند، نگاه کنید:

در مثال اول (a)، اندازهی «فاصلهی دوم کوچک» که در مثال (b) نشانداده شده، نیمپرده کاهش یافته و «فاصلهی دوم کاسته» ایجاد شده. درحالیکه در مثال آخر (d)، اندازهی فاصلهی مثال (c)، نیمپرده افزایش یافته و «فاصلهی دوم افزوده» ایجاد شدهاست.
در عمل، زیاد از «فاصلهی دوم کوچک» استفاده نمیشود، زیرا؛ نتها معادل یکدیگر (آنهارمونیک) میشوند.

با این وجود، «فاصلهی دوم افزوده»، اغلب در فاصلهی بین درجات ششم و هفتم گام «مینور هارمونیک» پدیدار میشود:
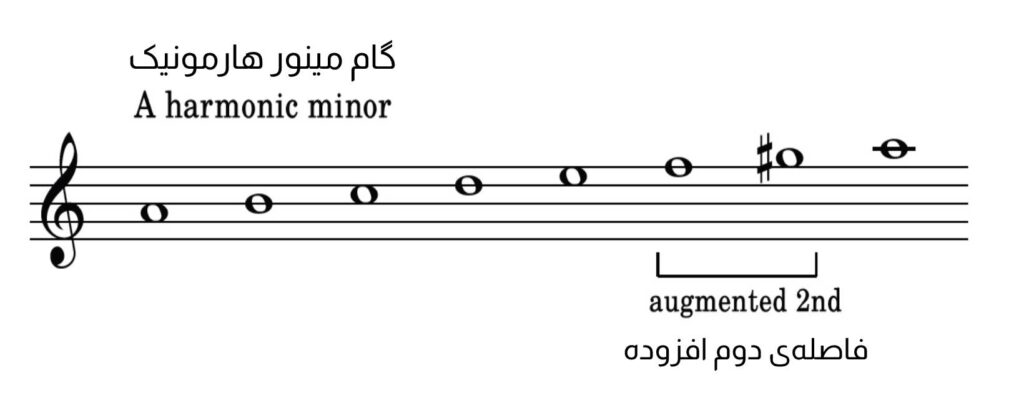
فواصل اونیسون، چهارم، پنجم و اکتاو (هشتم)، میتوانند پسوند کاسته، درست یا افزوده داشتهباشند.
اما فواصل دوم،سوم، ششم و هفتم، پسوندهای بزرگ، کوچک، کاسته یا افزوده را میگیرند.
شایان ذکر است که تغییر اندازهی فواصل، هم ازطریق نتِ بم و هم ازطریق نتِ زیر آن فاصله، امکانپذیر است. برای مثال، به فاصلهی تصویر زیر که در گام «سی مینور» نوشتهشده است، نگاه کنید:
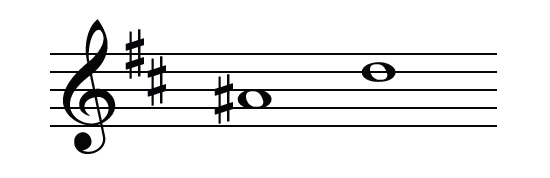
اگر نتِ بمِ این فاصله نت «لا» بود، فاصلهی بهدست آمده، «چهارم درست» میشد. اما از آنجاییکه نت «لا» به «لا دیز» آلتره شده و فاصله را نیمپرده کوچکتر کرده، این فاصله به فاصلهی «چهارم کاسته» تبدیل شدهاست.
برای نامگذاری فواصل، راحتتر است که به فاصلهی سادهتری که همان شمارهی فاصله را دارد، مراجعه کنیم. برای مثال: برای بهدست آوردن فاصلهی حقیقیِ دو نت، «فاصلهی چهارم درست» را درنظر می گیریم؛ یک «فاصلهی چهارم درست» با یک نیمپرده که به آن افزوده شده، «فاصلهی چهارم افزوده» را میسازد.
نمودار زیر، روابط فواصل با یکدیگر را نشان میدهد. فلشهایی که جهتشان به سمت راست است، نشاندهندهی این است که یک نیمپرده به فاصله افزوده شده. درحالیکه فلشهایی که جهتشان به سمت چپ است، نشاندهندهی این است که یک نیمپرده از فاصله کاسته شدهاست:
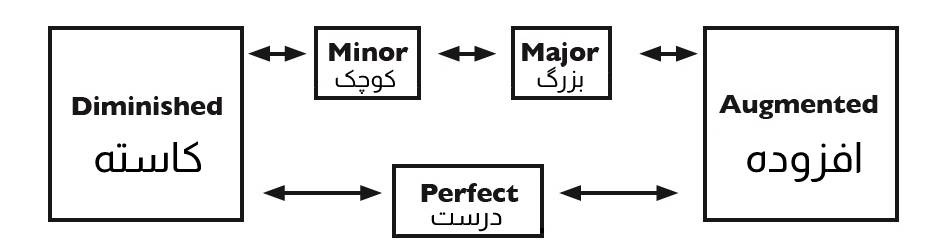
فواصل ترکیبی (Compound Intervals)
فواصلی که بزرگتر از یک اکتاو هستند را «فواصل ترکیبی» میگویند. فواصل ترکیبی را به دو صورت میتوان نامگذاری کرد:

موسیقیدانها معمولا در هنگام تمرین، بیشتر به فواصل نهم و یازدهم برمیخورند تا فواصل ترکیبی دوم یا چهارم درست. کلمهی «ترکیبی» (Compound) برای فواصلی که بزرگتر از دو اکتاو هستند نیز استفاده میشود. پس «فاصلهی دوم ترکیبی»، ممکن است یک فاصلهی دوم باشد که با یک یا چند اکتاو ترکیب شدهاست.
در آخرین مرحله، بهطور خلاصه از جنبهای صحبت میکنیم که برای نقش فواصل، بهعنوان بخشی بیانگر و نحوهای که به گوش میرسند؛ بسیار اهمیت دارد: مطبوعیت و نامطبوعی.
فواصل مطبوع و نامطبوع
مفهوم مطبوع (Consonant) یا نامطبوع (Dissonant) بودن فواصل، گاهی با واژه هایی چون؛ ملایم و ناملایم یا خوشایند و ناخوشایند نیز بیان میشود. (Rest-Unrest / Concord-Discord / Stability-Instabality)
فاصلهای مانند «فاصلهی سوم بزرگ» را مطبوع میگویند، چراکه صدای آن آرام و پایدار است. درحالیکه «فاصلهی چهارم افزوده» (Tritone) را نامطبوع بهحساب میآوریم، زیرا؛ صدای آن احساس تنشی را ایجاد میکند که بهدنبال حلشدن است.
مطبوع یا نامطبوع بودن درجات در موسیقی تونال، به بافت موسیقی و نظرشخصی فرد درمورد جنبههای بیانگر موسیقی بستگی دارد. همهی اینها کاملاً شخصی است. در طول قرنها نظرات متفاوتی درمورد آنچه نامطبوع تلقی میشود؛ وجود داشتهاست. اما بهطورکلی فواصل درست، ششم بزرگ و ششم کوچک، «مطبوع» درنظر گرفته میشوند و فواصل دوم بزرگ، دوم کوچک، هفتم بزرگ، هفتم کوچک و فواصل افزوده و کاسته، «نامطبوع» بهحساب میآیند.
فواصل نامطبوع، ازنظر میزان ناخوشایند بودن، با یکدیگر متفاوت هستند. این موضوع نیز موضوعی کاملاً شخصی است. اما درنهایت، تمامی این فواصل نامطبوع، صدایی ناکامل دارند و بهنوعی به حلشدن نیاز دارند.
برای مثال، با نواختن جفت نتهای زیر، به صدای حلشدن «فاصلهی چهارم افزوده» روی «فاصلهی ششم» گوش فرادهید:

این احساس تنش و رهایی، در قلبِ چیزی است که موسیقی را رسا و بیانگر میسازد. یکی از مثالهای کلاسیک، درمورد چگونگیِ حفظ کردن حس تعلیق و عدم ثبات، اپرای Tristanand Isolde، اثر «واگنر» است. جاییکه این مقدمهی معروف صحنه را طرحریزی میکند و با داشتن ابهام، آن حالت اشتیاق و آرزومندی را ایجاد میکند:

در اینجا، اولین آکورد به آکورد «تریستن» (Tristan chord) معروف است و شاید بتوان گفت که معروفترین آکورد در تمام موسیقی تونال غربی است.
فیلسوف «برایان مگی» (Bryan Magee) نوشتهاست که «آکورد تریستن» نه تنها یک، بلکه دو فاصلهی نامطبوع در خود دارد. همین موضوع در شنونده تمایلی مضاعف ایجاد میکند؛ تنشی دلهرهآور برای حلشدن.
آکوردی که به آن انتقال مییابد، یکی از این فواصل نامطبوع را حل میکند اما دیگری را برطرف نمیسازد و شما باید کمابیش تمام طول اپرا صبر کنید تا سرانجام حل شدن آن را بشنوید. (اما ارزش صبر کردن را دارد!)
بهجای فکرکردن به اصطلاحات دوگانهی مطبوع و نامطبوع، بهتر است که به این جنبه از فواصل با دید زنجیرهای نگاه کنیم. با گذشت زمان، همانطور که قاعدههای سیستم تونال، بیش از پیش، تحت فشار کروماتیسم قرن نوزدهم قرار گرفتند، (چنانکه در واگنر، اشتراوس و مالر شنیده شد) به ناچار تصور مردم از مطبوعیت و نامطبوعی تغییر کرد.
تضعیف سیستم تونال در طول قرن نوزدهم منجر به چیزی شد که گاهی اوقات «رهایی از نامطبوعی» (Emancipation of the dissonance) خوانده میشود.
این بدان معناست که فواصلی که قبلاً نامطبوع تلقی میشدند، میتوانستند بهعنوان واحدهایی مستقل، بدون احتیاج به حلشدن، وجود داشتهباشند و درعوض میشد با آنها طوری رفتار کرد که گویی مطبوع هستند.
این موضوع نهتنها در موسیقی آهنگسازان «مکتب دوم وین»، بلکه از قبل، در موسیقی «لیست»، «دبوسی» و جمع کثیر دیگر نیز صدق میکرد.
طبقهبندی «فاصلهی چهارم» آسان نیست، زیرا برخی مشخصههای «فاصلهی درست» را دارد و درعین حال نامطبوع بهشمار میرود. طبقهبندی آن تاحدودی به این بستگی دارد که، این فاصله، در کدام قسمت از بافت موسیقی قرار میگیرد. «فاصلهی چهارم»، خصوصا زمانی که با هارمونی اصلی درگیر شود یا در تعارض باشد و سپس حل شود، بسیار موثر است. وقتی این اتفاق رخ میدهد، «تعلیق» (Suspension) نامیده میشود. «تعلیق»ها، منبع اصلی ایجاد ناهماهنگی بیانگر، در بسیاری از موسیقیهای تونال، بهویژه موسیقیهای نوشتهشده در دورهی باروک هستند.
بهطور معمول، نتی که «معلق» است، روی ضرب قوی قرار میگیرد و روی ضرب ضعیف حل میشود.
روند ایجاد تعلیق سه قسمت دارد:
در مرحلهی اول، تهیه (آماده سازی) وجود دارد: درآن دو نت ثابت وجود دارند که با خط اتحاد بههم متصل میشوند و با ثابت ماندن نتها یا تعلیقشان، فاصلهی نامطبوع میان نت ثابت و هارمونی تغییریافتهی آکورد بعدی ایجاد میشود.
سرانجام هنگامیکه نت نگهداشته شده به سمت پایین حرکت میکند، حل شده و فاصلهی مطبوع ایجاد میشود. (نت محسوس به نت تونیک میرسد) مانند مثالی که در زیر آمده، هنگام تغییر هارمونی، معمولا نتی که فاصلهی نامطبوع روی آن حل میشود غایب است.

این یک تعلیق «۴ به ۳» (3-4) نام دارد. نام تعلیق از روی عدد فاصلهی نامطبوعی که روی نت باس تشکیل شده (در اینجا بین نت «ر» تا «سل») و فاصلهای که روی آن حل میشود بهدست میآید.
علاوهبر تعلیق «۴ به ۳» (3-4)، تعلیق «۷ به ۶» (6-7) و «۹ به ۸» (8-9) نیز وجود دارند. این تعلیقها ممکن است گاهی در «زنجیر»ها شنیده شوند. ( زنجیر (Chain): هنگامیکه حلِ یک تعلیق، شروع تعلیق بعد را میسازد.)
این وسیلهی موردعلاقهی استادان باروک ایتالیایی، مانند؛ کورلی (Corelli) و ویوالدی (Vivaldi) بود.
در جلسهی پنجم، نحوهی ساخت آکوردها و همچنین نحوهی نامگذاری آنها را با استفاده از روشهای مختلف میآموزیم.
اگر جلسات گذشته را از دست دادهاید، میتوانید آنها را در لیست زیر ببینید:
منبع: Pianist


آموزشتون فوقالعاده بود 👏👏👏👏